Reference


OpenAI's Answer
In topology, continuity and sequential continuity are related but distinct concepts.
-
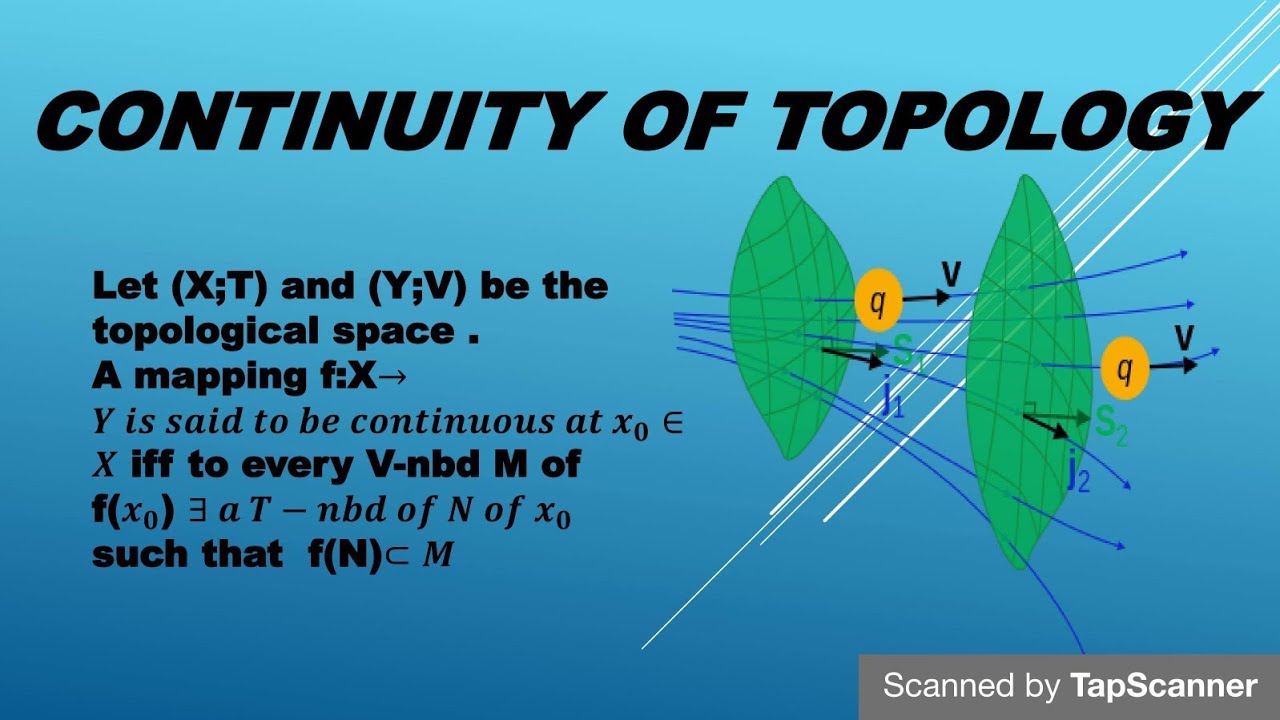
Continuity: A function ( f: X \rightarrow Y ) between two topological spaces is continuous if the pre-image of every open set in ( Y ) is an open set in ( X ). This is the general definition of continuity in topological spaces.
-
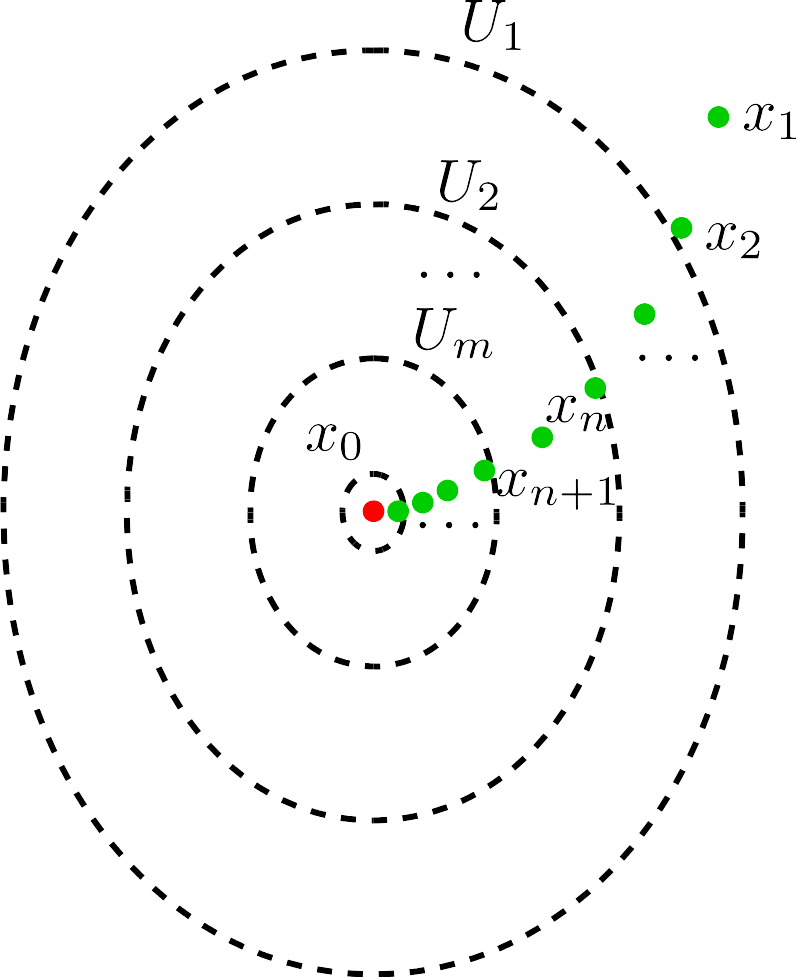
Sequential Continuity: A function is sequentially continuous at a point if, for every sequence converging to that point, the image of the sequence under the function converges to the image of the point.
Key Differences:
-
In metric spaces, which are a special kind of topological space, sequential continuity and continuity are equivalent. However, this is not generally true for all topological spaces.
-
For non-first-countable spaces, sequential continuity may not imply continuity. Spaces where the two concepts are equivalent are called sequential spaces.
For more details, you can explore the Wikipedia article on continuous functions or the discussion on Math StackExchange.

Follow Up
Related
How does a continuous function affect compactness and connectedness of sets?
What are the differences between continuous and uniformly continuous functions?
Why is the space of continuous functions on X considered a complete metric space?
For this privately held financial services company, a compelling journey of business transformation