Reference



Reference




Reference

OpenAI's Answer
Continuous functions have specific effects on compactness and connectedness of sets:
Compactness
-
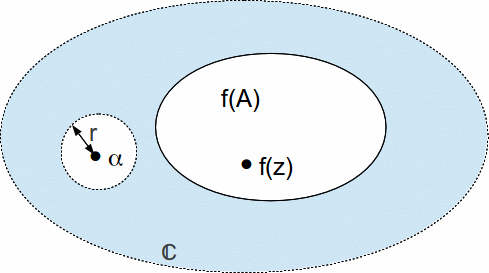
Preservation of Compactness: Continuous functions preserve compactness. This means that if you have a compact set in a topological space, the image of this set under a continuous function is also compact. This is because the continuous image of a compact set remains compact.
Sources:
Connectedness
-
Preservation of Connectedness: Continuous functions also preserve connectedness. If a set is connected in its original space, its image under a continuous function will be connected in the target space. This is linked to the property that continuous functions map connected spaces to connected spaces.
Sources:
These properties are fundamental in topology and have many applications in mathematical analysis and related fields.
Follow Up
Related
How does Donald Trump's win affects Indian students preparing for graduate studies in US?
How does the law affect members of the Armed Forces, CSIS, or RCMP?
CHAPTER 2 - Literature Review 2.1. Introduction This chapter undertakes a review of literature to
How much area was affected by fires between 1998 and 2001?
How does the BDNF polymorphism affect extinction learning in both mice and humans?