Reference

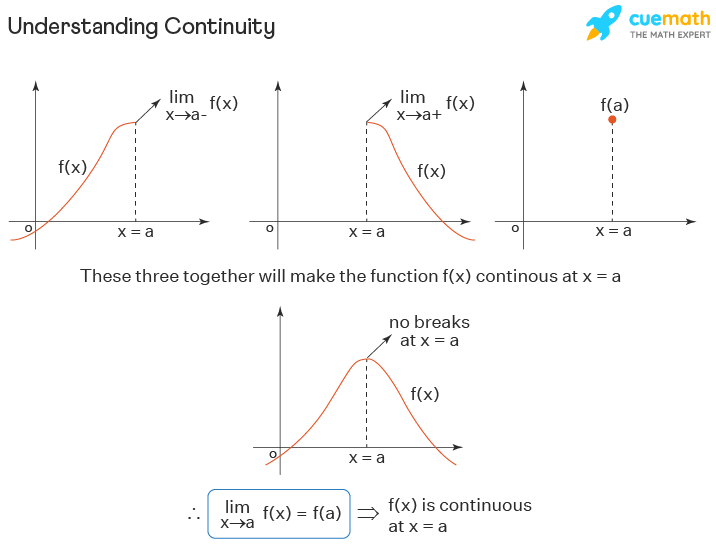
Continuous Functions. In calculus, a continuous function is a real-valued function whose graph does not have any breaks or holes. Continuity lays the foundational groundwork for the intermediate value theorem and extreme value theorem. They are in some sense the ``nicest" functions possible, and many proofs in real analysis rely on ...

A function f(x) is said to be a continuous function in calculus at a point x = a if the curve of the function does NOT break at the point x = a. The mathematical definition of the continuity of a function is as follows. A function f(x) is continuous at a point x = a if

In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as discontinuities.More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument.