How does a continuous functor in category theory relate to small limits?
Reference
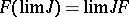



OpenAI's Answer
In category theory, a continuous functor is one that preserves all small limits. This means if a functor ( F: C \rightarrow D ) is continuous, then for any diagram ( A: E \rightarrow C ) within ( C ), the limit of ( A ) being preserved under ( F ) implies:
[ F(\lim A) \cong \lim (F \circ A) ]
This relationship essentially means that the structure of limits, when transformed by a continuous functor, remains intact. This concept is utilized when the category ( C ) has all small limits, making it a complete category.
For more information, you can visit Wikipedia or read about it on the nLab.