Reference

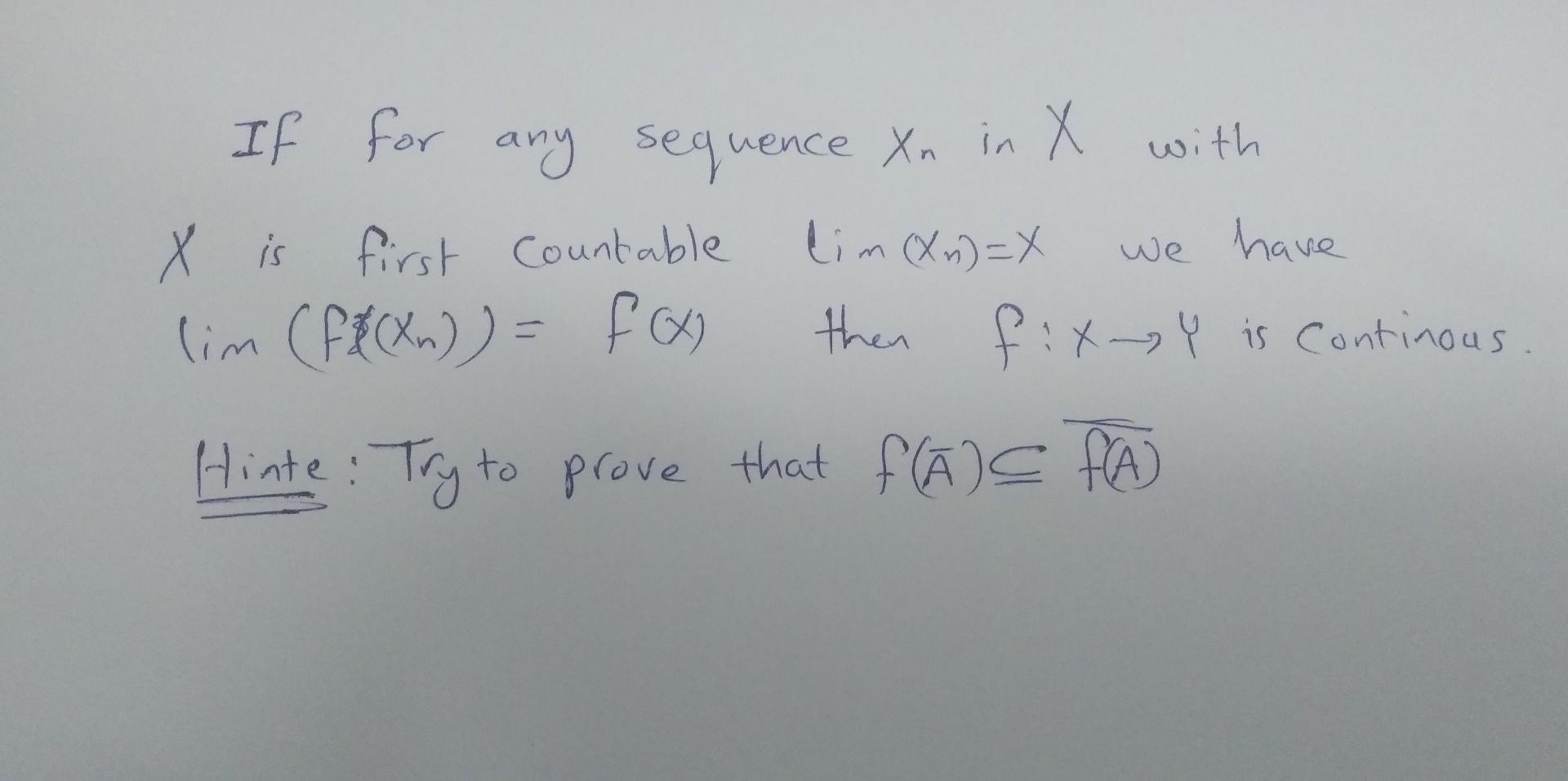


OpenAI's Answer
In a first-countable space, the relationship between sequential continuity and continuity is more straightforward. A topological space is first-countable if each point has a countable base of neighborhoods. This property allows us to use sequences to test continuity.
Key Points:
-
First-Countable Spaces:
- A space is first-countable if every point has a countable local base (a countable collection of open sets where every neighborhood of the point contains one of these sets).
- First-countable spaces include all metric spaces.
-
Sequential and General Continuity:
- In a first-countable space, sequential continuity (where the limit of ( f(x_n) ) equals ( f(\lim x_n) ) for every sequence ( x_n ) converging to a point ( x )) implies general continuity.
- Conversely, general continuity implies sequential continuity regardless of the space.
-
Importance of First-Countability:
- The implication from sequential continuity to general continuity doesn't necessarily hold in spaces that are not first-countable.
- In first-countable spaces, convergence can be checked using sequences, making the two concepts equivalent.
For more details, you can check this Math Stack Exchange post or other resources related to first-countability properties.
Follow Up
Related
How does Donald Trump's win affects Indian students preparing for graduate studies in US?
How much area was affected by fires between 1998 and 2001?
Can the loss of smell sensitivity affect eating habits and obesity?
How do markers of inflammation and Vitamin E affect peripheral nervous system function?
What actions did the Joint Boundary Commission take to address concerns of residents in affected hom